Stochastik IV: 40 Karten, 41 oder 42?

Tatsächlich ist es nun länger als ein halbes Jahr her, als mein siebzigster Artikel sich zuletzt mit Wahrscheinlichkeitsrechnung im Yu-Gi-Oh! TCG befasste. Ein mehr als nur guter Grund dafür war, dass ich entweder zu leichte oder zu schwierige (Zonk, 37,5% der Posts in dem Thread sind von mir) Artikel über die Stochastik geschrieben habe und nie so wirklich ein optimales Mittelmaß finden konnte.

Doch kürzlich habe ich mir überlegt, wie ein effektives Side Deck der neuen Liste der verbotenen und limiterten Karten wohl aussehen könnte, und wie wichtig es ist, bestimmte Karten daraus möglichst schnell zu ziehen. Angeblich sollen ja nun die Lightsworns das Metagame dominieren (gut - unwahrscheinlich ist das nicht), und da diese aus offensichtlichen Gründen bevorzugt den unlimitierten Königlicher Erlass im Main Deck spielen werden (oder zumindest im Side, um darauf umboarden), wird man neben Lichteinsperrender Spiegel womöglich auch noch auf Twister zurückgreifen müssen, oder auf Monster wie Chiron der Magier, die auch gegen potenziell gestärkte Burner-Decks effektiv sind. Aber dann habe ich mir die Frage gestellt: "Wie wahrscheinlich ist es denn eigentlich, dass ich die wichtigen Anti-Karten rechtzeitig auf dem Feld habe, bevor ich von gemillten Wulfs, unterstützt von Celestias (und eben Royal Decree), überrannt werde und beim Konterangriff nicht durch die Necro Gardnas durchkomme?". Und dies wiederum ist nicht nur abhängig davon, wie oft ich diese Anti-Karten von meinem Side Deck zur Verfügung gestellt bekomme, sondern womöglich auch von der Anzahl der Karten, die ich im Main Deck spiele!

Um herauszufinden, ob man so aus einem Side Deck noch mehr Effizienz herausholen kann, wollte ich mich in meinem heutigen Artikel stochastisch dieser inzwischen uralten Diskussion widmen: Wie gut es denn nun wirklich ist, nur 40 Karten im Main Deck zu spielen. Denn oftmals - du kennst das sicherlich auch - möchte ich aus meinen spontanen Deckideen einfach keine (Tech-)Karten mehr kicken, um an die Untergrenze von 40 Karten zu gelangen, und würde am liebsten 41 oder gar 42 (oder noch mehr) beibehalten.

Lektüre, die ihr zwingend gelesen haben müsst, um die Rechnungen in diesem Artikel zu verstehen:

• Stochastik I: Einführung in die Stochastik

• Stochastik II: 'Gewinne' und 'Nieten'

Als Zusatzlektüre würde noch Stochastik III: Anwendungen in YGO dienen, allerdings braucht ihr die letzten Aufgaben nicht zu können. Es ist aber wie gesagt empfehlenswert beziehungsweise notwendig, zumindest die ersten beiden Artikel nochmal kurz überflogen zu haben. Wenn euch nicht interessiert, wie ich auf die später folgenden Tabellenwerte komme, dann lest die Artikel von mir aus auch gar nicht und vertraut mir einfach.

Um ein grobes Gefühl dafür zu bekommen, inwieweit die Anzahl der Karten im Main Deck überhaupt relevant für diese ganze Geschichte ist, habe ich einige Werte in die Teilmengen-Formel aus Teil 2 meiner Artikelserie eingesetzt - und kam zu folgenden Ergebnissen:

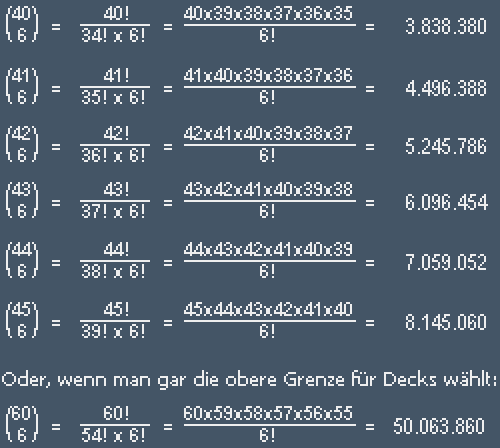
Die großen Zahlen hier bedeuten die Anzahlen der Möglichkeiten, eine 6-Karten-Starthand aus einem 40- bzw. 41-, 42-, ..., 60-Karten-Deck zu ziehen. Verhältnismäßig betrachtet lassen sich gerade zwischen 40 (3,8 Millionen Möglichkeiten), 41 (4,5 Millionen) und 42 Karten (5,2 Millionen) keine "allzu großen" Unterschiede ausmachen, während hingegen bei den höheren Deckkartenanzahlen die Anzahl der Möglichkeiten geradezu zu explodieren scheint - bestes Beispiel hierfür ist das 60-Karten-Deck, wo ich bereits 50 Millionen Möglichkeiten habe, eine Starthand herauszuziehen. Das sind fast viermal so viele Möglichkeiten wie man einen Lottoschein (ohne Zusatz- und Superzahl) ausfüllen kann!

Die Anzahl der Möglichkeiten ist für uns jedoch keine Größenordnung, mit der wir in solchen Diskussionen arbeiten können. Wir benötigen prozentuale Wahrscheinlichkeiten, mit welchen theoretische Szenarien eintreten. Diese erhalten wir, sobald wir bestimmte Angaben machen, die unsere Starthand erfüllen soll. Denn für diese Angaben ergibt sich dann ebenso wieder eine Anzahl an Möglichkeiten - und wenn wir diese Anzahl durch die 6-Karten-Starthand-Möglichkeiten teilen, so erhalten wir solche brauchbaren Prozentwerte (siehe auch Teil 3 dieser Artikelserie).

Als sehr anschauliches Beispiel für die Optimierung deines Decks kann man das "Gadget-Problem" herbeiziehen. Woraus besteht ein Gadget-Deck im Optimalfall? Na klar - aus den 9 Gadgets (je 3x Roter Apparat, Grüner Apparat und Gelber Apparat), 2 Ultimate Offering und massig Monster-Removal, damit ich mit meinen Gadgets durchkomme und mein erwirtschaftetes Plus auch auf dem Spielfeld wirksam machen kann!

... nicht!

Letztere Punkte stimmen zwar teils, aber bei der Gadget-Anzahl ist 9 mathematisch gesehen eben NICHT die optimale Anzahl der kleinen Maschinen! In Japan spielte man die Gadget-Decks aus Effizienzgründen ab und zu mit nur 8 (ja, acht wie "AchtDukeAcht") Gadgets. Das ist schon etwas merkwürdig - denn wenn man einen Apparat nur zweimal im Deck hat, kann man später im Spiel einen weniger suchen als wenn man ihn dreimal zur Verfügung hätte.

Warum spielten die Leute also unlogischerweise nur 8 statt 3x3 Gadgets? Diese Tatsache sollen die folgenden Tabellen klären:

Auffällig ist hier auf jeden Fall, dass die Wahrscheinlichkeit, genau 1 Gadget zu ziehen, mit zunehmender Deckkartenanzahl steigt. Recht paradox, aber das liegt an der in kleineren Decks eingeschränkten Möglichkeit, Nicht-Gadget-Karten zu ziehen. Mit 9 aus 40 Karten machen die Apparate immerhin 22,5 % des gesamten Decks aus, womit automatisch auch die Wahrscheinlichkeit, ausschließlich andere Karten zu ziehen, sinkt.

Weil jedoch somit die Wahrscheinlichkeit, 2 oder mehr Apparate zu ziehen, höher ist als in größeren Decks, ist in kleineren Decks die Wahrscheinlichkeit, mindestens einen Gadget zu ziehen, zunehmend größer. Beispielsweise kann man in einem 60-Karten-Deck mit einer Wahrscheinlichkeit von 36,0 %, also quasi in jedem 3. Spiel - eher öfter (2,8) -, ohne Gadgets auf der Hand ins Spiel gehen. Und das ist ja bekanntermaßen nicht so optimal! In 40-Karten-Decks sieht dies schon besser aus, denn mit einer Wahrscheinlichkeit von 19,2 % gehst du erst in jedem rund 5. Spiel, Tendenz sinkend (5,2), leer aus. Deswegen greift man in Gadget-Decks in jedem Fall zu kleinen, überschaubaren Decks, um jene Gefahr zu minimieren.

Allerdings lässt sich die Wahrscheinlichkeit, exakt 1 Apparat auf die 6-Karten-Starthand zu ziehen, durchaus noch optimieren: Denn wenn du wenigere Exemplare der Maschinen spielst, so steigt die Wahrscheinlichkeit, dass du mehr Nicht-Gadget-Karten auf die Starthand bekommst, was statistisch gesehen verhindert, dass du zu oft mit 2 oder gar mehr Gadgets starten musst. Und dies ist in Zeiten, in welchen kaum noch Pullings gespielt werden, ziemlich suboptimal, da man eigentlich ungerne das ganze Spiel durch mit 1 toten Apparat auf der Hand rumläuft. Lieber den einen Gadget weniger und dafür ein Removal mehr auf der Hand haben. Und zudem eben langsamer Gefahr laufen, dass in der Mitte des Spiels die Gadgets im Deck ausgehen und die Such-Effekte nutzlos werden, weil die Hälfte davon auf deiner Hand liegen.

Betrachten wir zur Verdeutlichung dieses Gedankenganges folgende Tabelle:

Das in der Tabelle fett markierte Maximum von 43,5 % sagt aus, dass du bei einer Anzahl von 6 Apparaten in einem 40-Karten-Deck die höchste Wahrscheinlichkeit erreicht hast, genau 1 davon auf der Starthand zu halten. Allerdings gehst du - wie bei 9 Gadgets in einem 60-Karten-Deck - mit einer Wahrscheinlichkeit von 35,0 % in jedem dritten Spiel leer aus!

Daher muss hier ein "Zwischending" gefunden werden: Wir benötigen eine Gadget-Anzahl, die eine sehr hohe Quote aufweist, überhaupt einen Apparat auf die Starthand zu ziehen - und dem entgegen auch eine recht niedrige, 2 oder mehr der kleinen Maschinen aufzunehmen. Aus diesem Grund habe ich eine weitere Zeile an die Tabelle angefügt, mittels derer wir leichter erkennen können, welche Anzahlen somit in Frage kommen. Durch einen kurzen Vergleich der Wahrscheinlichkeiten von "mindestens 1" und "mindestens 2" sind dies nämlich 7 oder 8.

Bei einer Anzahl von 8 Gadgets bleibt am Ende der "Gadget-Ketten" häufiger ein größerer Rest übrig als bei 7 Gadgets ^[1], zudem hat man bei 8 in jedem 2,9-ten Spiel 2 oder mehr Gadgets auf der Starthand. Dem entgegen steht aber das Argument, dass man bei 7 Gadgets dennoch eine Quote von "jedem 3,5-ten Spiel" hat - welche auch nicht wesentlich vernachlässigbarer ist. Außerdem zieht man bei 7 in jedem 3,5-ten Spiel keinen Apparat auf die Hand - bei 8 jedoch nur in jedem 4,2-ten Spiel - und ich habe lieber einen toten Gadget auf der Hand als gar keinen! Dies lässt uns zum Entschluss kommen, dass es am sinnvollsten ist, 8 Apparate ins Deck zu packen statt der blauäugigen 9. Das freut uns auch, denn dann haben wir mehr Slots für Removal oder eventuell das zweite Ultimate Offering!

(Und da Matches üblicherweise sowieso maximal 3 Spiele lange andauern, ist es wohl ohnehin sinnvoller, auf das negative Ereignis in "jedem 4(,2). Spiel" zurückzugreifen als auf das, das zwischen 3 und 4 steht. Außerdem spielt man ja noch gerne Pot of Avarice, weshalb es in seltenen Situationen - z.B. gegen Makrokosmos - schon entscheidend sein kann, ob man nun 7 oder 8 Gadgets spielt.)

Doch genug von den Gadgets! Ich wollte mich doch noch meinem ursprünglichen Gedanken widmen:

Das ist hier die Frage. Decks bauen grundsätzlich auf vielen verschiedenen Kombos auf, welche wiederum durch weitere Kombos hervorgerufen werden. Ein Beispiel hierfür sind die traditionellen First-Turn-Kill-Decks rund um Magical Scientist und Catapult Turtle: Diese beiden Schlüsselkarten, die den Gegner (gemeinsam mit nem Mystic Wok oder Poison of the Old Man) erledigen, werden durch Last Will und Monster Reborn/Premature Burial/Reasoning/Monster Gate hervorgebracht, welche wiederum vorher durch eine "Ziehmaschine" (Draw Engine) (Gruß ans E!) aus dem Deck geholt werden müssen, die sich erneut aus vielen kleinen Combos zusammenstellen lässt (3x Toon Table of Contents + Toon Cannon Soldier zum Beispiel).

Im Advanced Format schaut das ganze natürlich schon wieder anders aus, da durch die Limitierung oder das Verbot bestimmter Schlüsselkarten nur noch wenige oder gar keine so "schnellen" Kombos mehr gespielt werden können. Dadurch, dass es weniger schnelle Ziehmaschinen gibt (wobei man Inzahlungnahme natürlich mal wieder auf 3 gelassen hat... solche Spaken), ist das Potenzial, dass ein One Turn Kill gelandet wird, wesentlich geringer - und somit braucht man sich eigentlich nicht mehr so viele Gedanken darum zu machen, bestimmte Karten möglichst schon auf der Starthand zu haben.

Und somit ist es - besonders in sehr "control-lastigen Decks" (also in Decks, in denen viel mit Kontrolle gearbeitet wird und weniger auf die Geschwindigkeit) - auch nicht immer notwendig, unbedingt 40 Karten zu spielen.

Dennoch kann man die Wahrscheinlichkeiten für einzelne Karten betrachten. Einige Twilight-Builds werden ja beispielsweise - Lichtbrigarde sei Dank - auf einen frühen Chaos Sorcerer hoffen. Welchen Unterschied macht es hier, mehr als 40 Karten zu spielen?

Der Ausschlag ist wirklich nur sehr gering. Man hat den Chaos Sorcerer bei einer Deckgröße zwischen 40 und 43 Karten in rund jedem 7. Spiel (6,7 - 7,1) auf der Hand; erst ab 44 Karten (7,4) bis schlussendlich zu 60 Karten (10,0) tut sich was. Das Gerücht, man zieht Karten definitiv wahrscheinlicher auf die Starthand, wenn man 40 Karten im Deck spielt, ist hiermit so ziemlich entkräftet.

Doch wie sieht das ganze aus, wenn es plötzlich um mehr als nur 1 Schlüsselkarte geht? Hier kommen wir zurück zu meinem Side Deck, das Karten gegen die bereits jetzt unbeliebten Lichtverpflichteten beinhalten soll: Lichteinsperrender Spiegel und Twister. Die folgende Tabelle listet die Wahrscheinlichkeiten für jeweils 1 Karte auf, da eine für beide Karten jegliche Rahmen sprengen würde.

Aus dieser Tabelle wird ersichtlich, dass die Wahrscheinlichkeit, gewisse Karten auf die Starthand zu ziehen, in einem Bereich nahe der unteren 40er-Grenze weitaus weniger von der Deckkartenanzahl abhängt als von der Anzahl der Exemplare, die im Deck gespielt werden!

Nach dem Sideboarden mindestens einen von 3 reingeboardeten Lichtspiegel zu ziehen, geschieht in einem 40-Karten-Deck in jedem 2,5-ten Spiel; bei einem 41-Karten-Deck in jedem 2,6-ten. Das macht nicht wirklich einen Unterschied - vielleicht höchstens dann, wenn man einen Vergleich mit dem 60-Karten-Deck anstellt (wo man die Karte dann "nur" in jedem 3,6-ten Spiel sofort zieht).

Auch Kombinationen von geboardeten Karten sind von der Deckkarten-Anzahl ziemlich unbetroffen: In einem 40-Karten-Deck nach dem Sideboarden sowohl Twister (um einen potenziellen Decree zu beseitigen) als auch Lichtspiegel je mindestens einmal auf die Starthand zu ziehen, wird in jedem 7,2-ten Spiel vorkommen, wenn man beide 3-mal reinboardet; in einem 42-Karten-Deck in jedem 7,8-ten; und in einem 60-Karten-Deck in jedem 15,1-ten Spiel (bevor du das Suchen anfängst: diese Werte sind nicht aus der Tabelle ablesbar).

Beachtlich jedoch sind die Schwankungen, die durch die unterschiedliche Anzahl der Exemplare der Karten entstehen, die du hineingeboardet hast. Hast du nur 2 Lichtspiegel im Side, ziehst du nach dem Boarden von deinem 40-Karten-Deck statistisch gesehen erst in jedem 3,6-ten Spiel mindestens einen davon - anstatt in jedem 2,5-ten bei 3 Spiegeln im Side.

Auch die gedachten Kombinationen von Karten müssen ordentlich darunter leiden, wenn du ihren Sideboard-Platz von je 3 auf 2 herunterschraubst: So hast du - statt in jedem 7,2-ten Spiel - beide Karten erst in jedem 14,5-ten (!!!) Spiel jeweils mindestens einmal auf der Starthand! Und Ziel eines effizienten Sideboards soll es ja wohl sein, Schwächen des eigenen Decks möglichst geschwind auszugleichen, um ein verloren geglaubtes Match noch einmal zu wenden und in ein drittes Spiel zu bringen.

Mh ja klar - ein Fazit zum Schluss ist immer recht öde. Vor allem, weil ich mir an deiner Stelle dann denken würde "Warum hab ich den Artikel überhaupt gelesen und nicht einfach ins Fazit geglotzt?". Vielleicht hast du das auch so gemacht. Spielt ja auch keine Rolle, denn wir haben heute viel gelernt:

Der Gadget-Sachverhalt sollte dir klar gemacht haben, dass es wichtig ist, die 40-Karten-Grenze bei Gadget-Decks nicht zu überschreiten und gleichzeitig nur 8 statt 9 möglichen Apparaten zu spielen, damit die Ausbeute der idealen Starthände möglichst groß ist und man sich nur selten mit toten Starthänden rumschlagen muss.

Zudem ist es in heutigen Decks nahezu vollkommen irrelevant, ob man nun 40, 41 oder 42 Karten im Deck hat. Relevant werden die Veränderungen der Ziehwahrscheinlichkeiten erst dann, wenn man in die höheren Vierziger geht (@ lorric: Gemeint ist die Kartenzahl des Decks! Hehehehe. :P ) - oder dann, wenn man ein OTK-Deck gebaut hat und eine hohe Wahrscheinlichkeit auf das Treffen der "Ziehmaschine" benötigt. Spielt man jedoch auf Kontrolle, kann man gut und gerne auch 41-44 Karten ins Deck packen.

Auch auf ein gutes Side Deck hat die Anzahl der Deckkarten kaum Auswirkungen. Sofern - versteht sich - keine absolut lebenswichtige Kombo (wie beispielsweise bei OTK-Decks) vorhanden ist, denn hier zählt jeder Prozent. Wichtig beim Bau des Side Decks ist es, abzuwägen, wie häufig / schnell man eine Karte benötigt, wenn man sie reinboardet.

Hat man vor, zwischen den Spielen eh lediglich eine Tech-Karte aus dem Side ins Deck zu packen, um den Gegner zusätzlich zu peinigen (z.B. einen Schaufelbrecher, um den Gegner zu finishen, weil er unter Messenger of Peace, Level Limit - Area B, und Crush Card Virus durch angreifen kann, er nicht von Skill Drain betroffen ist - oder man aber sogar Limiter Removal auf ihn spielen kann!), so braucht man sie auch nicht öfter als 1- oder 2-mal dort zu spielen.

Ist eine Karte jedoch essentiell, um gegen ein Deck zu überleben (Schattenspiegel gegen Twilight, Lichtspiegel gegen Lightsworns), so sollte man sie am besten 3-mal ins Side Deck nehmen und auch stets komplett ins Deck boarden, da 2 oder gar nur 1 Exemplar der Karte ihren Schutz-Effekt nicht erfüllen kann (mal abgesehen davon, dass nach 1 Heavy Storm oder MST auf die Karte sowieso dann Feierabend wäre).

Falls man in einem Main Deck mehr als 40 Karten hat und auf gewisse Karten problemlos verzichten kann, so sollte man die Anzahl der Deckkarten selbstverständlich auf 40 halten. Werden jedoch gewisse zusätzliche Slots gebraucht, weil man beispielsweise noch 3-mal Feierliches Urteil spielen möchte, ist dies - wie bereits weiter oben erwähnt - kein größeres Problem.

Kleiner Tipp: Wer die Corn'schen 41 Karten im Main Deck spielt, macht sich mehr als nur cheatverdächtig. Wer jenen Pile Shuffle kennt, mittels welchem man das Deck exakt in seine ursprüngliche, vorher sortierte Reihenfolge zurückversetzen kann, obwohl es komplett durchgemischt aussieht, sollte wissen, wovon ich rede!

Als ich gestern kurz vom FT-Sieger Umut Serin angeschrieben wurde und ihm einen kurzen Spoiler über meinen heutigen Artikel genannt habe, hat er mir spontan einen Teil eines Artikels (ein paar Tabellen) herausgesucht, den er vor ewiger Zeit mal auf der Seite seiner Kassel Corporation gelesen hatte.

Obwohl ich schon sehr weit geschrieben hatte, so haben mir die Tabellen ein wenig geholfen, meinen Artikel besser zu strukturieren. Somit möchte ich Umut und dem Urheber jenes Artikels, yosuke, herzlich danken!

Übrigens: Umut ist der einzige bekanntere, auf eTCG aktive Spieler, der NICHT in seiner Signatur oder sonstwo in seinem Profil mit Titeln prollt...

Außerdem ist er sehr "tierlieb" (Insider) und generell sowieso sympathisch. So stellt man sich den "perfekten" YGO-Spieler vor... von daher wird Umut diese Woche mal gehyped, so dass sich hoffentlich jeder mal ne Scheibe von ihm abschneidet!

(Und von Claudio, aber der hat ja schon "länger" nix mehr gerissen, daher lasst das mal lieber sein! :P :P :P )

Wie auch letzte Woche habe ich mit diesem Artikel unsere Kolumnenschreiber-Vorgabe von ca. 1.400 Wörtern bei weitem gesprengt, denn es waren jeweils etwa 3.000. Toby schreibt auch stets über 2.000 Wörter, manchmal ebenso mehr, und dann kommt immer wieder dieser Herr Chronos und meint, hier einfach mal so 4.000 Wörter zu schreiben... grauenvoll ist das, wie sollen wir nur jemals wieder auf unseren Standard zurückkehren können! =(

Ich bin mal gespannt, wie meine/unsere nächsten Artikel mit 1.500 Wörtern dann von euch angenommen werden......

("Wöööh, der war ja viel zu kurz!!" v_v)

Greets,

Harti

• Gadget-Kette mit 8 (z.B. 3 Grünen, 3 Gelben und 2 Roten) Apparaten,

  1.) Gelb-Grün-Rot-Gelb-Grün-Rot-Gelb-Grün // Rest: 0

  2.) Grün-Rot-Gelb-Grün-Rot-Gelb-Grün // Rest: Gelb

  3.) Rot-Gelb-Grün-Rot-Gelb-Grün // Rest: Gelb-Grün

  (Wahrscheinlichkeit für Kette 3 ist gering, da nur 2x Red Gadget enthalten ist)

  
  

• Gadget-Kette mit 7 (z.B. 3 Grünen, 2 Gelben und 2 Roten) Apparaten,

  1.) Gelb-Grün-Rot-Gelb-Grün-Rot // Rest: Grün

  2.) Grün-Rot-Gelb-Grün-Rot-Gelb-Grün // Rest: 0

  3.) Rot-Gelb-Grün-Rot-Gelb-Grün // Rest: Grün

  (Wahrscheinlichkeit für Ketten 1 und 3 sind gering, da nur 2x Yellow Gadget und 2x Red Gadget gespielt werden)

... wonach es eigentlich sinnvoller sein müsste, mit 7 zu spielen.